Урок и презентация на тему: "Число e. Функция. График. Свойства"
Дополнительные материалы
Уважаемые пользователи, не забывайте оставлять свои комментарии, отзывы, пожелания! Все материалы проверены антивирусной программой.
Обучающие пособия и тренажеры в интернет-магазине "Интеграл" для 11 класса
Интерактивное пособие для 9–11 классов "Тригонометрия"
Интерактивное пособие для 10–11 классов "Логарифмы"
Ребята, сегодня мы будем изучать особенное число. Оно занимает отдельное место во "взрослой" математике и имеет много замечательных свойств, некоторые из которых мы и рассмотрим.
Вернемся к показательным функциям $y=a^x$, где $а>1$. Мы можем построить множество различных графиков функций для различных оснований.
Но следует заметить, что:
- все функции проходят через точку (0;1),
- при $х→-∞$ график имеет горизонтальную асимптоту $у=0$,
- все функции возрастают и выпуклы вниз,
- а также непрерывны, что в свою очередь означает, что они дифференцируемы.
Рассмотрим функцию $y=2^x$ и построим к ней касательную.
Аккуратно построив наши графики, можно заметить, что угол наклона касательной равен 35°.
Теперь давайте построим график функции $y=3^x$ и также построим касательную:

В этот раз угол наклона касательной приблизительно равен 48°. Вообще, стоит заметить: чем больше основание показательной функции, тем больше угол наклона.
Особый интерес представляет касательная с углом наклона равным 45°. К графику какой показательной функции можно провести такую касательную в точке (0;1)?
Основание показательной функции должно быть больше 2, но меньше 3, так как требуемый угол касательной достигается где-то между функциями $y=2^x$ и $y=3^x$. Такое число было найдено и оно оказалось довольно уникальным.
Показательную функцию, у которой касательная, проходящая через точку (0;1) имеет угол наклона равный 45°, принято обозначать: $y=e^x$
.
Основание нашей функции является иррациональным числом. Математиками было выведено приблизительное значение этого числа $e=2.7182818284590…$.
В курсе школьной математике принято округлять до десятых, то есть $e=2.7$.
Давайте построим график функции $y=e^x$ и касательную к этому графику.

Нашу функцию принято называть экспоненциальной.
Свойства функции $y=e^x$.
1. $D(f)=(-∞;+∞)$.
2. Не является ни четной, ни нечетной.
3. Возрастает на всей области определения.
4. Не ограничена сверху, ограничена снизу.
5. Наибольшего значения нет, наименьшего значения нет.
6. Непрерывна.
7. $E(f)=(0; +∞)$.
8. Выпукла вниз.
В высшей математике доказано, что экспоненциальная функция всюду дифференцируема, и ее производная равна самой функции: $(e^x)"=e^x$.
Наша функция находит большое применение в многих разделах математики (в математическом анализе, в теории вероятности, в программировании), и многие реальные объекты связаны с этим числом.
Пример.
Найти касательную к графику функции $y=e^x$ в точке $х=2$.
Решение.
Уравнение касательной описывается формулой: $y=f(a)+f"(a)(x-a)$.
Последовательно найдем требуемые значения:
1. $f(a)=f(2)=e^2$.
2. $f"(a)=e^a$.
3. $f"(2)=e^2$.
4. $y=f(a)+f"(a)(x-a)=e^2+e^2(x-2)=e^2*x-e^2$.
Ответ: $y=e^2*x-e^2$
Пример.
Найти значение производной функции $y=e^{3x-15}$ в точке $х=5$.
Решение.
Давайте вспомним правило дифференцирования функции вида $y=f(kx+m)$.
$y"=k*f"(kx+m)$.
В нашем случае $f(kx+m)=e^{3x-15}$.
Найдем производную:
$y"=(e^{3x-15})"=3*e^{3x-15}$.
$y"(5)=3*e^{15-15}=3*e^0=3$.
Ответ: 3.
Пример.
Исследовать на экстремумы функцию $y=x^3*e^x$.
Решение.
Найдем производную нашей функции
$y"=(x^3*e^x)"=(x^3)"*e^x+x^3(e^x)"=3x^2*e^x+x^3*e^x=x^2*e^x(x+3)$.
Критических точек у функции нет, так как производная существует при любом х.
Приравняв производную к 0, получаем два корня: $x_1=0$ и $x_2=-3$.
Отметим наши точки на числовой прямой:

Задачи для самостоятельного решения
1. Найти касательную к графику функции $y=e^{2x}$ в точке $х=2$.2. Найти значение производной функции $y=e^{4x-36}$ в точке $х=9$.
3. Исследовать на экстремумы функцию $y=x^4*e^{2x}$.

Учитель математики МОУ
«Мултановская СОШ»
Маханова Самига Галимжановна
с. М у л т а н о в о
Февраль 2011г.
Тема урока: «Число е. Производная показательной функции».
Цель: Ввести понятие «экспоненты» , «натурального логарифма», сформировать понятие о производной показательной функции у = е х, первообразной показательной функции.
Образовательная:
Повторить и углубить знания по теме «Показательная функция. Свойства показательной функции»;
Повторить правила дифференцирования функции;
Познакомить учащихся с понятием «экспоненты» (числа е);
Познакомить учащихся с формулами производной показательной функции у = а х и у = а кх +b ;
Познакомить с формулой первообразной показательной функции;
Формировать навыки вычисления производной показательной функции, пользуясь правилами и формулами дифференцирования.
Развивающая:
Развивать и совершенствовать применение правил дифференцирования
для показательной функции;
Научить учащихся применять электронные информационные технологии при обучении и подготовке к урокам математики.
Повышать графическую культуру учащихся;
Содействовать развитию умений осуществлять самооценку учебной деятельности.
Воспитательная:
Создавать для учащихся положительную мотивацию к уроку математики путем вовлечения каждого в активную деятельность;
Воспитывать потребность оценивать свою деятельность и работу товарищей;
Помочь осознать ценности совместной работы;
Воспитывать у учащихся аккуратность, культуру математической речи.
Оборудование к уроку:
Компьютерный класс (8 ноутбуков +1ноутбук для демонстрации), проектор, презентация, раздаточный материал.
Ход урока:
Организация урока, объявление темы и цели урока:
Сегодня на уроке мы изучаем новую тему «Производная показательной функции». Наша цель: (Слайд2.) познакомиться с понятием «экспоненты», «натурального логарифма», с теоремой о дифференцировании показательной функции и научиться выполнять дифференцирование показательной функции.
Эпиграфом к нашему уроку я выбрала стихи Б. Слуцкого: (слайд 3.)
…Показательная функция
Не случайно родилась,
В жизнь органически влилась
И движением прогресса занялась.
Б. Слуцкий
I. Актуализация опорных знаний:
Устная фронтальная работа с классом:
Сформулируйте определение показательной функции (Слайд 5.)
Перечислите по графику основные свойства показательной функции.
(Слайд 6)
Свойства показательной функции: (слайд 4)
Область определения функции
Область значений показательной функции
График функции с осью ОУ пересекается в точке (0;1) и не пересекается с осью ОХ.
Показательная функция принимает положительные значения на всей числовой прямой.
Перечислите свойства показательной функции при а 1.
Перечислите свойства показательной функции при 0 .
Дайте определение производной функции в точке х 0 . (слайд 7)
Сформулируйте геометрический смысл производной. (слайд 8)
А сейчас вспомним правила дифференцирования функций:
2) Игра «Найди пары». (слайд 9.)
Для формул из первого столбика найдите правильные ответы из второго столбика и прочитайте слово из третьего столбика. Устно, с комментированием.
| (u +v)" | cos x | E |
| (u v)" | n x n-1 | П |
| (u / v)" | -1 / sin 2 x | А |
| (x n)" | Sin x | Н |
| C" | u" v + u v" | К |
| (Cu)" | 1 / cos 2 x | Т |
| (sin x)" | (u "v - u v") / v 2 | С |
| (cos x)" | 0 | О |
| (tg x)" | u" + v" | Э |
| (ctg x)" | C u" | Н |
| Э | u" + v" | (u +v)" |
| К | u" v + u v" | (u v)" |
| С | (u "v - u v") / v 2 | (u / v)" |
| П | n x n-1 | (x n)" |
| О | 0 | C" |
| Н | C u" | (Cu)" |
| Е | Cos x | (sin x)" |
| Н | -Sin x | (cos x)" |
| Т | 1 / cos 2 x | (tg x)" |
| А | -1 / sin 2 x | (ctg x)" |
Проверьте свой ответ по таблице: (слайд 10 )
II .Изучение новой темы:
1) Исследовательская работа с помощью ЭОР ресурсов за ноутбуками. Работа в паре.
Откройте в Интернете Цифровые образовательные ресурсы по алгебре и началам анализа 11 класс тема: «Производные показательной функции, числа е и натурального логарифма.» модуль И1
Внимательно ознакомьтесь с каждым элементом Модуля, запишите в тетрадях основные формулы, ознакомьтесь с их доказательствами.
Выполните задания для самоконтроля. Проверьте итог своих работ по «Статистике» (С).
План работы по модулю:
Показательная функция с основанием е. – (Знакомство с экспонентой)
Формула производной показательной функции. – (Вывод формулы производной функции у = е х)
Задание для самоконтроля. – (тест с выбором ответа)
Определение натурального логарифма ln. – (ln x = log e x)
Формула производной показательной функции. – (вывод формулы производной показательной формулы)
Задание для самоконтроля. – (Задание с кратким ответом)
Первообразная показательной функции – (вывод формулы производной показательной функции)
Задание для самоконтроля – (тест с выбором ответа)
2)
C
л. 15-18
Фронтальный опрос, по изученному материалу. Первичное закрепление материала. Применение формул производной показательной функции.
(e х )" = e х ;
(e кх + b )" = k e kx + b ;
(a x )" = a x ∙ ln a ;
(a kx + b )" = k a Kx +b ∙ ln a
F(a
x
) =
Ученик работает самостоятельно у доски:
Решение: f(x) = x 2 * 2 –x; D(f) = R; f " = 2x * 2 –x – x 2 * 2 -x ln2, D(f) =R ,
2x * 2 –x – x 2 * 2 –x ln2 = 0;
X * 2 -x (2 – x * ln 2) = 0; - min + max - f " (x)
X * 2 –x = 0 ; 2 – x * ln x = 0 2 – x > 0, x = 0; 2 – x * ln2 = 0 0 2/ln2 f(x)
Ответ: х max = 2 / ln2; x min = 0
Самостоятельная работа обучающего характера:
Самостоятельная работа в паре за ноутбуками. Интерактивный модуль П1 «производная показательной функции. Число е. Натуральный логарифм». – тест из 5 заданий. При открытии модуля на каждом компьютере выходят разные задания.
V.Итог урока: Что нового вы узнали на уроке?
Какие моменты урока для вас были наиболее интересными?
Кто доволен своей работой на уроке?
VI. Домашнее задание: п. 41 ; № 539(а,б,г); 540(в); 542(а,б); 544(б).
Интерактивный тест с компьютером. Свойства показательной функции К1.
На рабочем столе каждого компьютера откройте Модуль Cл. 11
«Свойства показательной функции К1». Нажмите «мышкой» на «воспроизвести модуль». Вам выйдет тест из 5 заданий.
Выполните 1 -задание Модуля, нажмите «мышкой» на номер верного ответа или запишите ответ в тесте. Нажмите «мышкой » на «ответить» и переходите к другому заданию.
Если выполнили задание неверно, откройте подсказку,
найдите ошибку в своем решении.
Проверьте итог своих работ по «Статистике» (С).
График показательной функции представляет собой кривую плавную линию без изломов, к которой в каждой точке, через которую она проходит, можно провести касательную. Логично предположить, что если можно провести касательную, значит функция будет дифференцируема в каждой точке своей области определения.
Отобразим в одних координатных осях несколько графиков функции y = x a , Для а = 2; a = 2,3; a = 3; a = 3,4.
В точке с координатами (0;1). Углы наклона этих касательных будут равны приблизительно 35, 40, 48 и 51 градусов соответственно. Логично предположить, что на интервале от 2 до 3 существует число, при котором угол наклона касательной будет равен 45 градусов.
Дадим точную формулировку этого утверждения: существует такое число большее 2 и меньшее 3, обозначаемое буквой е, что показательная функция y = e x в точке 0, имеет производную равную 1. То есть: (e ∆x -1) / ∆x стремится к 1 при стремлении ∆х к нулю.
Данное число e является иррациональным и записывается в виде бесконечной непериодической десятичной дробью:
e = 2,7182818284…
Так как число е положительно и отлично от нуля, то существует логарифм по основанию e. Данный логарифм называется натуральным логарифмом . Обозначается ln(x) = log e (x).
Производная показательной функции
Теорема: Функция e x дифференцируема в каждой точке своей области определения, и (e x)’ = e x .
Показательная функция a x дифференцируема в каждой точке своей области определения, и причем (a x)’ = (a x)*ln(a).
Следствием из этой теоремы является тот факт, что показательная функция непрерывна в любой точке своей области определения.
Пример: найти производную функции y = 2 x .
По формуле производной показательной функции получаем:
(2 x)’ = (2 x)*ln(2).
Ответ: (2 x)*ln(2).
Первообразная показательной функции
Для показательной функции a x заданной на множестве вещественных чисел первообразной будет являться функция (a x)/(ln(a)).
ln(a) - некоторая постоянная, тогда (a x / ln(a))’= (1 / ln(a)) * (a x) * ln(a) = a x для любого х. Мы доказали эту теорему.
Рассмотрим пример на нахождение первообразной показательной функции.
Пример: найти первообразную к функции f(x) = 5 x . Воспользуемся формулой приведенной выше и правилами нахождения первообразных. Получим: F(x) = (5 x) / (ln(5)) +C.
Цели урока: сформировать представление о числе е ; доказать дифференцируемость функции в любой точке х ;рассмотреть доказательство теоремы о дифференцируемости функции ; проверка сформированности умений и навыков при решении примеров на их применение.
Задачи урока.
Образовательная: повторить определение производной, правила дифференцирования, производную элементарных функций, вспомнить график и свойства показательной функции, сформировать умение нахождения производной показательной функции, осуществить контроль знаний с помощью проверочного задания и теста.
Развивающая: способствовать развитию внимания, развитию логического мышления, математической интуиции, умению анализировать, применять знания в нестандартных ситуациях.
Воспитательная: воспитывать информационную культуру, выработать навыки работы в группе и индивидуально.
Методы обучения: словестный, наглядный, деятельный.
Формы обучения: коллективная, индивидуальная, групповая.
Оборудование: учебник “Алгебра и начала анализа” (под редакцией Колмогорова), все задания группы В “Закрытый сегмент” под редакцией А.Л. Семенова, И.В.Ященко, мультимедийный проектор.
Этапы урока:
- Сообщение темы, цели, задач урока (2мин.).
- Подготовка к изучению нового материала через повторение раннее изученного (15 мин.).
- Ознакомление с новым материалом (10 мин.)
- Первичное осмысление и закрепление новых знаний (15 мин.).
- Задание на дом (1 мин.).
- Подведение итогов (2 мин.).
Ход урока
1. Организационный момент.
Объявляется тема урока: “Производная показательной функции. Число е.”, цели, задачи. Слайд 1. Презентация
2. Активизация опорных знаний.
Для этого на I этапе урока ответим на вопросы и решим задачи на повторение. Слайд 2.
У доски два ученика работают по карточкам, выполняя задания типа В8 ЕГЭ.
Задание для первого ученика:
Задание для второго ученика:

Остальные учащиеся выполняют самостоятельную работу по вариантам:
| Вариант 1 | Вариант 2 | ||
| 1. |  |
1. |  |
| 2. |  |
2. |  |
| 3. |  |
3. |  |
| 4. |  |
4. |  |
| 5. |  |
5. |  |
Пары обмениваются решениями и проверяют работы друг у друга, сверяясь сответами по слайду 3.
Рассматриваются решения и ответы учащихся, работающих у доски.
Проверка домашнего задания №1904. Демонстрируется слайд 4.
3. Актуализация темы урока, создание проблемной ситуации.
Учитель просит дать определение показательной функции и перечислить свойства функции у = 2 х. Графики показательных функций изображаются в виде гладких линий, к которым в каждой точке можно провести касательную. Но существование касательной к графику функции в точке с абсциссой х 0 равносильно её дифференцируемости в х 0.
Для графиков функции у = 2 x и у = 3 x проведем к ним касательные в точке с абсциссой 0. Углы наклона этих касательных к оси абсцисс приблизительно равны 35° и 48° соответственно. Слайд 5.
Вывод: если основание показательной функцииа увеличивается от 2 до, например, 10, то угол между касательной к графику функции в точки х=0 и осью абсцисс постепенно увеличивается от 35° до 66,5°. Логично предположить, что существует основание а , для которого соответствующий угол равен 45
Доказано, что существует такое число большее 2 и меньшее 3.. Его принято обозначать буквой е . В математике установлено, что число е – иррациональное, т.е. представляет собой бесконечную десятичную непериодическую дробь.
е = 2,7182818284590…
Замечание (не очень серьезное). Слайд 6.
На следующем слайде 7 появляется портреты великих математиков – Джона Непера, Леонарда Эйлера и краткая справка о них.
- Рассмотреть свойства функции у=e x
- Доказательство теоремы 1. Слайд 8.
- Доказательство теоремы 2. Слайд 9.
4. Динамическая пауза или разрядка для глаз.
(Исходное положение - сидя, каждое упражнение повторяется 3-4 раза):
1. Откинувшись назад, сделать глубокий вдох, затем, наклонившись вперед, выдох.
2. Откинувшись на спинку стула, прикрыть веки, крепко зажмурить глаза, не открывая век.
3. Руки вдоль туловища, круговые движения плечами назад и вперёд.
5. Закрепление изученного материала.
5.1 Решение упражнений №538, №540, №544в.
5.2 Самостоятельное применение знаний, умений и навыков. Проверочная работа в форме теста. Время выполнения задания – 5 мин.
Критерии оценки:
“5” – 3 балла
“4” – 2 балла
“3” - 1 балл
6. Подведение итогов и результатов работы на уроке.
- Рефлексия.
- Выставление оценок.
- Сдача тестовых заданий.
7. Задание на дом: п. 41 (1, 2); № 539 (а, б, г); 540 (в, г), 544 (а, б).
“Закрытый сегмент” №1950, 2142.
При
выводе самой первой формулы таблицы
будем исходить из определения
производнойфункции в точке. Возьмем ,
где x
–
любое действительное число, то есть, x
–
любое число из области определения
функции .
Запишем предел отношения приращения
функции к приращению аргумента при :
![]()
Следует заметить, что под знаком предела получается выражение , которое не являетсянеопределенностью ноль делить на ноль, так как в числителе находится не бесконечно малая величина, а именно ноль. Другими словами, приращение постоянной функции всегда равно нулю.
Таким образом, производная постоянной функции равна нулю на всей области определения .
Производная степенной функции.
Формула
производной степенной функции имеет
вид ![]() ,
где показатель степени p
–
любое действительное число.
,
где показатель степени p
–
любое действительное число.
Докажем сначала формулу для натурального показателя степени, то есть, для p = 1, 2, 3, …
Будем
пользоваться определением производной.
Запишем предел отношения приращения
степенной функции к приращению
аргумента:

Для
упрощения выражения в числителе обратимся
к формуле бинома
Ньютона:
Следовательно,

Этим доказана формула производной степенной функции для натурального показателя.
Производная показательной функции.
Вывод формулы производной приведем на основе определения:
Пришли к неопределенности. Для ее раскрытия введем новую переменную , причем при . Тогда . В последнем переходе мы использовали формулу перехода к новому основанию логарифма.
Выполним
подстановку в исходный предел:

Если
вспомнить второй
замечательный предел, то придем к
формуле производной показательной
функции:
Производная логарифмической функции.
Докажем
формулу производной логарифмической
функции для всех x
из
области определения и всех допустимых
значениях основания a
логарифма.
По определению производной имеем:

Как
Вы заметили, при доказательстве
преобразования проводились с использованием
свойств логарифма. Равенство  справедливо
в силу второго замечательного предела.
справедливо
в силу второго замечательного предела.
Производные тригонометрических функций.
Для вывода формул производных тригонометрических функций нам придется вспомнить некоторые формулы тригонометрии, а также первый замечательный предел.
По
определению производной для функции
синуса имеем ![]() .
.
Воспользуемся
формулой разности синусов:

Осталось
обратиться к первому замечательному
пределу:

Таким образом, производная функции sin x есть cos x .
Абсолютно
аналогично доказывается формула
производной косинуса.

Следовательно, производная функции cos x есть –sin x .
Вывод
формул таблицы производных для тангенса
и котангенса проведем с использованием
доказанных правил дифференцирования
(производная
дроби).
Производные гиперболических функций.
Правила
дифференцирования и
формула производной показательной
функции из таблицы производных позволяют
вывести формулы производных гиперболического
синуса, косинуса, тангенса и котангенса.

Производная обратной функции.
Чтобы при изложении не было путаницы, давайте обозначать в нижнем индексе аргумент функции, по которому выполняется дифференцирование, то есть, - это производная функции f(x) по x .
Теперь сформулируем правило нахождения производной обратной функции.
Пусть
функции y
= f(x)
и x
= g(y)
взаимно
обратные, определенные на
интервалах и соответственно.
Если в точке существует
конечная отличная от нуля производная
функции f(x)
,
то в точке существует
конечная производная обратной
функции g(y)
,
причем ![]() .
В другой записи
.
В другой записи ![]() .
.
Можно
это правило переформулировать для
любого x
из
промежутка ,
тогда получим  .
.
Давайте проверим справедливость этих формул.
Найдем
обратную функцию для натурального
логарифма ![]() (здесь y
–
функция, а x
-
аргумент). Разрешив это уравнение
относительно x
,
получим (здесь x
–
функция, а y
–
ее аргумент). То есть,
(здесь y
–
функция, а x
-
аргумент). Разрешив это уравнение
относительно x
,
получим (здесь x
–
функция, а y
–
ее аргумент). То есть, ![]() и взаимно
обратные функции.
и взаимно
обратные функции.
Из таблицы
производных видим,
что ![]() и
и ![]() .
.
Убедимся,
что формулы нахождения производных
обратной функции приводят нас к этим
же результатам:

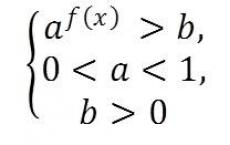 Решение показательных неравенств
Решение показательных неравенств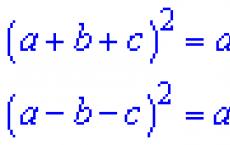 Формулы сокращенного умножения
Формулы сокращенного умножения Химия - комплексная подготовка к внешнему независимому оцениванию
Химия - комплексная подготовка к внешнему независимому оцениванию