Для того что бы упростить алгебраические многочлены, существуют формулы сокращенного умножения . Их не так уж и много и они легко запоминаются, а запомнить их нужно. Обозначения которые используются в формулах, могут принимать любой вид (число или многочлен).
Первая формула сокращенного умножения называется разность квадратов
. Она заключается в том что из квадрата одного числа отнимается квадрат второго числа равен величине разности данных чисел, а также их произведению.
а 2 - b 2 = (а - b)(a + b)
Разберем для наглядности:
22 2 - 4 2 = (22-4)(22+4)=18 * 26 = 468
9а 2 - 4b 2 c 2 = (3a - 2bc)(3a + 2bc)
Вторая формула о сумме квадратов . Звучит она как, сумма двух величин в квадрате равняется квадрату первой величины к ней прибавляется двойное произведение первой величины умноженное на вторую, к ним прибавляется квадрат второй величины.
(а + b) 2 = a 2 +2ab + b 2
Благодаря данной формуле, становится намного проще вычислять квадрат от большого числа, без использования вычислительной техники.
Так к примеру:
квадрат от 112 будет равен
1) В начале разберем 112 на числа квадраты которых нам знакомы
112 = 100 + 12
2) Вписываем полученное в скобки возведенные в квадрат
112 2 = (100+12) 2
3) Применяя формулу, получаем:
112 2 = (100+12) 2 = 100 2 + 2 * 100 * 12 + 122 = 10000 + 2400+ 144 = 12544
Третья формула это квадрат разности
. Которая гласит о том, что две вычитаемые друг друга величины в квадрате равняются, тому что, от первой величины в квадрате отнимаем двойное произведение первой величины умноженное на вторую, прибавляя к ним квадрат второй величины.
(а +b) 2 = а 2 - 2аb + b 2
где (а - b) 2 равняется (b - а) 2 . В доказательство чему, (а-b) 2 = а 2 -2аb+b 2 = b 2 -2аb + а 2 = (b-а) 2
Четвертая формула сокращенного умножения называется куб суммы . Которая звучит как: две слагаемые величины в кубе равны кубу 1 величины прибавляется тройное произведение 1 величины в квадрате умноженное на 2-ую величину, к ним прибавляется тройное произведение 1 величины умноженной на квадрат 2 величины, плюс вторая величина в кубе.
(а+b) 3 = а 3 + 3а 2 b + 3аb 2 + b 3
Пятая, как вы уже поняли называется куб разности
. Которая находит разности между величинами, как от первого обозначения в кубе отнимаем тройное произведение первого обозначения в квадрате умноженное на второе, к ним прибавляется тройное произведение первого обозначения умноженной на квадрат второго обозначения, минус второе обозначение в кубе.
(а-b) 3 = а 3 - 3а 2 b + 3аb 2 - b 3
Шестая называется - сумма кубов
. Сумма кубов равняется произведению двух слагаемых величин, умноженных на неполный квадрат разности, так как в середине нет удвоенного значения.
а 3 + b 3 = (а+b)(а 2 -аb+b 2)
По другому можно сказать сумму кубов можно назвать произведение в двух скобках.
Седьмая и заключительная, называется разность кубов
(ее легко перепутать с формулой куба разности, но это разные вещи). Разность кубов равняется произведению от разности двух величин, умноженных на неполный квадрат суммы, так как в середине нет удвоенного значения.
а 3 - b 3 = (а-b)(а 2 +аb+b 2)
И так формул сокращенного умножения всего 7, они похожи друг на друга и легко запоминаются, единственно важно не путаться в знаках. Они так же рассчитаны на то, что их можно использовать в обратном порядке и в учебниках собрано довольно много таких заданий. Будьте внимательны и все у вас получится.
Если у вас появились вопросы по формулам, обязательно пишите их в комментариях. Будем рады ответить вам!
Если Вы находитесь в декретном отпуске, но хотите зарабатывать деньги. Просто перейдите по ссылке Интернет бизнес с Орифлейм . Там все очень подробно написано и показано. Будет интересно!
Математические выражения (формулы) сокращённого умножения (квадрат суммы и разности, куб суммы и разности, разность квадратов, сумма и разность кубов) крайне не заменимы во многих областях точных наук. Эти 7 символьных записей не заменимы при упрощении выражений, решении уравнений, при умножении многочленов, сокращении дробей , решении интегралов и многом другом. А значит будет очень полезно разобраться как они получаются, для чего они нужны, и самое главное, как их запомнить и потом применять. Потом применяя формулы сокращенного умножения на практике самым сложным будет увидеть, что есть х и что есть у. Очевидно, что никаких ограничений для a и b нет, а значит это могут быть любые числовые или буквенные выражения.
И так вот они:
Первая х 2 - у 2 = (х - у) (х+у) .Чтобы рассчитать разность квадратов двух выражений надо перемножить разности этих выражений на их суммы.
Вторая (х + у) 2 = х 2 + 2ху + у 2 . Чтобы найти квадрат суммы двух выражений нужно к квадрату первого выражения прибавить удвоенное произведение первого выражения на второе плюс квадрат второго выражения.
Третья (х - у) 2 = х 2 - 2ху + у 2 . Чтобы вычислить квадрат разности двух выражений нужно от квадрата первого выражения отнять удвоенное произведение первого выражения на второе плюс квадрат второго выражения.
Четвертая (х + у) 3 = х 3 + 3х 2 у + 3ху 2 + у 3. Чтобы вычислить куб суммы двух выражений нужно к кубу первого выражения прибавить утроенное произведение квадрата первого выражения на второе плюс утроенное произведение первого выражения на квадрат второго плюс куб второго выражения.
Пятая (х - у) 3 = х 3 - 3х 2 у + 3ху 2 - у 3 . Чтобы рассчитать куб разности двух выражений необходимо от куба первого выражения отнять утроенное произведение квадрата первого выражения на второе плюс утроенное произведение первого выражения на квадрат второго минус куб второго выражения.
Шестая х 3 + у 3 = (х + у) (х 2 - ху + у 2) Чтобы высчитать сумму кубов двух выражений нужно умножить суммы первого и второго выражения на неполный квадрат разности этих выражений.
Седьмая х 3 - у 3 = (х - у) (х 2 + ху + у 2) Чтобы произвести вычисление разности кубов двух выражений надо умножить разность первого и второго выражения на неполный квадрат суммы этих выражений.
Не сложно запомнить, что все формулы применяются для произведения расчетов и в противоположном направлении (справа налево).
О существовании этих закономерностей з нали еще около 4 тысяч лет тому назад. Их широко применяли жители древнего Вавилона и Египта. Но в те эпохи они выражались словесно или геометрически и при расчетах не использовали буквы.
Разберем доказательство квадрата суммы (а + b) 2 = a 2 +2ab +b 2 .
Первым эту математическую закономерность доказал древнегреческий учёный Евклид, работавший в Александрии в III веке до н.э., он использовал для этого геометрический способ доказательства формулы, так как буквами для обозначения чисел не пользовались и учёные древней Эллады. Ими повсеместно употреблялись не “а 2 ”, а “квадрат на отрезке а”, не “ab”, а “прямоугольник , заключенный между отрезками a и b”.
Применяют для упрощения вычислений, а также разложение многочленов на множители, быстрого умножения многочленов. Большинство формул сокращенного умножения можно получить из бинома Ньютона - в этом Вы скоро убедитесь.
Формулы для квадратов применяют в вычислениях чаще. Их начинают изучать в школьной программе начиная с 7 класса и до конца обучения формулы для квадратов и кубов школьники должны знать на зубок.

Формулы для кубов не сильно сложные и их нужно знать при сведении многочленов к стандартному виду, для упрощения подъема суммы или разности переменной и числа к кубу.

Формулы обозначены красным получают из предыдущих группировкой подобных слагаемых.
Формулы для четвертого и пятого степени в школьном курсе мало кому пригодятся, однако есть задачи при изучении высшей математики где нужно вычислять коэффициенты при степенях.

Формулы для степени
n
расписаны
через биномиальные коэффициенты с использованием факториалов следующие

Примеры применения формул сокращенного умножения
Пример 1. Вычислить 51^2.
Решение.
Если есть калькулятор то без проблем находите
Это я пошутил - с калькулятором мудрые все, без него... (не будем о грустном).
Не имея калькулятора и зная приведенные выше правила квадрат числа находим по правилу
Пример 2. Найти 99^2.
Решение.
Применим вторую формулу
Пример 3.
Возвести в квадрат выражение
(x+y-3).
Решение. Сумму первых двух слагаемых мысленно считаем одним слагаемым и по второй формуле сокращенного умножения имеем

Пример 4.
Найти разность квадратов
11^2-9^2.
Решение. Поскольку числа небольшие то можно просто подставить значения квадратов
Но цель у нас совсем другая - научиться использовать формулы сокращенного умножения для упрощения вычислений. Для этого примера применим третью формулу
Пример 5.
Найти разность квадратов
17^2-3^2
.
Решение. На этом примере Вы уже захотите изучить правила чтобы вычисления свести к одной строке
Как видите - ничего удивительного мы не делали.
Пример 6.
Упростить выражение
(x-y)^2-(x+y)^2.
Решение.
Можно раскладывать квадраты, а позже сгруппировать подобные слагаемые. Однако можно прямо применить разность квадратов
Просто и без длинных решений.
Пример 7.
Возвести в куб многочлен
x^3-4.
Решение
. Применим 5 формулу сокращенного умножения
Пример 8.
Записать в виде разности квадратов или их сумме
а) x^2-8x+7
б) x^2+4x+29
Решение. а) Перегруппируем слагаемые

б) Упрощаем на основе предыдущих рассуждений
Пример 9.
Разложить рациональную дробь
Решение.
Применим формулу разности квадратов![]()
Составим систему уравнений для определения констант
К утроенному первому уравнению добавим второе. Найденное значение подставляем в первое уравнение![]()
Окончательно разложение примет вид ![]()
Разложить рациональную дробь часто необходимо перед интегрированием, чтобы снизить степень знаменателя.
Пример 10.
Используя бином Ньютона расписать
выражение (x-a)^7.
Решение. Что такое бином Ньютона Вы вероятно уже знаете. Если нет то ниже приведены биномиальные коэффициенты

Они образуются следующим образом: по краю идут единицы, коэффициенты между ними в нижней строке образуют суммированием соседних верхних. Если ищем разницу в каком-то степени, то знаки в расписании чередуются от плюса к минусу. Таким образом для седьмого порядка получим такой расклад

Внимательно также посмотрите как меняются показатели - для первой переменной они уменьшаются на единицу в каждом следующем слагаемом, соответственно для второй - на единицу растут. В сумме показатели всегда должны быть равны степени разложения (=7 ).
Думаю на основе приведенного выше материала Вы сможете решить задачи на бином Ньютона. Изучайте формулы сокращенного умножения и применяйте везде, где это может упростить вычисления и сэкономит время выполнения задания.
В предыдущем уроке мы разобрались с разложением на множители. Освоили два способа: вынесение общего множителя за скобки и группировку. В этом уроке - следующий мощный способ: формулы сокращённого умножения . В краткой записи - ФСУ.
Формулы сокращённого умножения (квадрат суммы и разности, куб суммы и разности, разность квадратов, сумма и разность кубов) крайне необходимы во всех разделах математики. Они применяются в упрощении выражений, решении уравнений, умножении многочленов, сокращении дробей, решении интегралов и т.д. и т.п. Короче, есть все основания разобраться с ними. Понять откуда они берутся, зачем они нужны, как их запомнить и как применять.
Разбираемся?)
Откуда берутся формулы сокращённого умножения?
Равенства 6 и 7 записаны не очень привычно. Как бы наоборот. Это специально.) Любое равенство работает как слева направо, так и справа налево. В такой записи понятнее, откуда берутся ФСУ.
Они берутся из умножения.) Например:
(a+b) 2 =(a+b)(a+b)=a 2 +ab+ba+b 2 =a 2 +2ab+b 2
Вот и всё, никаких научных хитростей. Просто перемножаем скобки и приводим подобные. Так получаются все формулы сокращённого умножения. Сокращённое умножение - это потому, что в самих формулах нет перемножения скобок и приведения подобных. Сокращены.) Сразу дан результат.
ФСУ нужно знать наизусть. Без первых трёх можно не мечтать о тройке, без остальных - о четвёрке с пятёркой.)
Зачем нужны формулы сокращённого умножения?
Есть две причины, выучить, даже зазубрить эти формулы. Первая - готовый ответ на автомате резко уменьшает количество ошибок. Но это не самая главная причина. А вот вторая...
Если Вам нравится этот сайт...
Кстати, у меня есть ещё парочка интересных сайтов для Вас.)
Можно потренироваться в решении примеров и узнать свой уровень. Тестирование с мгновенной проверкой. Учимся - с интересом!)
можно познакомиться с функциями и производными.
Формулы сокращенного выражения очень часто применяются на практике, так что их все желательно выучить наизусть. До этого момента нам будет служить верой и правдой , которую мы рекомендуем распечатать и все время держать перед глазами:
Первые четыре формулы из составленной таблицы формул сокращенного умножения позволяют возводить в квадрат и куб сумму или разность двух выражений. Пятая предназначена для краткого умножения разности и суммы двух выражений. А шестая и седьмая формулы используются для умножения суммы двух выражений a и b на их неполный квадрат разности (так называют выражение вида a 2 −a·b+b 2 ) и разности двух выражений a и b на неполный квадрат их суммы (a 2 +a·b+b 2 ) соответственно.
Стоит отдельно заметить, что каждое равенство в таблице представляет собой тождество . Этим объясняется, почему формулы сокращенного умножения еще называют тождествами сокращенного умножения.
При решении примеров, особенно в которых имеет место разложение многочлена на множители , ФСУ часто используют в виде с переставленными местами левыми и правыми частями:

Три последних тождества в таблице имеют свои названия. Формула a 2 −b 2 =(a−b)·(a+b) называется формулой разности квадратов , a 3 +b 3 =(a+b)·(a 2 −a·b+b 2 ) - формулой суммы кубов , а a 3 −b 3 =(a−b)·(a 2 +a·b+b 2 ) - формулой разности кубов . Обратите внимание, что соответствующим формулам с переставленными частями из предыдущей таблицы фсу мы никак не назвали.
Дополнительные формулы
В таблицу формул сокращенного умножения не помешает добавить еще несколько тождеств.
Сферы применения формул сокращенного умножения (фсу) и примеры
Основное предназначение формул сокращенного умножения (фсу) объясняется их названием, то есть, оно состоит в кратком умножении выражений. Однако сфера применения ФСУ намного шире, и не ограничивается кратким умножением. Перечислим основные направления.
Несомненно, центральное приложение формулы сокращенного умножения нашли в выполнении тождественных преобразований выражений . Наиболее часто эти формулы используются в процессе упрощения выражений .
Пример.
Упростите выражение 9·y−(1+3·y) 2 .
Решение.
В данном выражении возведение в квадрат можно выполнить сокращенно, имеем 9·y−(1+3·y) 2 =9·y−(1 2 +2·1·3·y+(3·y) 2) . Остается лишь раскрыть скобки и привести подобные члены: 9·y−(1 2 +2·1·3·y+(3·y) 2)= 9·y−1−6·y−9·y 2 =3·y−1−9·y 2 .
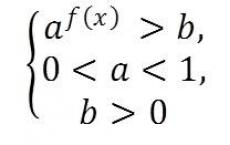 Решение показательных неравенств
Решение показательных неравенств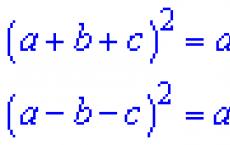 Формулы сокращенного умножения
Формулы сокращенного умножения Химия - комплексная подготовка к внешнему независимому оцениванию
Химия - комплексная подготовка к внешнему независимому оцениванию